兵棋推演的作战结构初探

『兵棋综合讨论区』Discussion 『兵棋学院』Wargame College
1

孙景伟在《战役矛盾运动规律研究》一书中，给出了两个陈述：

战斗所包含的一系列武器装备系统对抗行动的性质、数量及它们之间在目的、时间、空间上的关系，就是“战斗结构”．
战役所包含的一系列作战行动及其联系称为“战役结构”．

为了论述方便，我们统一称之为“作战结构”．从定义的共性上看，作战结构由对抗行动和行动之间的关系两者构成．一言以蔽之，在兵棋推演这个范畴中，无外乎也要研究推演中的对抗行动和行动之间的关系．关于这一个命题，我已经在《B4M人机对战机器蓝方先手首轮推演分析》一文中作了详细的论述．

《战役矛盾运动规律研究》一书完成了文本角度的理性总结，但缺乏从定性到定量的指导意见，怎样从定性到定量地确认对抗行动及其联系，怎样引入到兵棋推演领域之中，首先需要对兵棋的可解释性进行实践论和认识论的改造，使得在推演当中确立辩证法的语言．关于这一个命题，我已经在《兵棋的可解释性》一文中作了详细的论述．

是否将蕴含军事辩证法的理论研究引入到兵棋推演之中，就是没有前途的形而上学分析呢？首先来说，如果我国的兵棋理论与蕴含军事辩证法的理论研究是割裂的，那么凭什么判定在这样的兵棋理论指导下的推演，能够符合中国军事战略思维呢？其次来说，如果只是觉得“升华”一些一般性的理论或者从哲学的高度审视兵棋，是在用教科书关键词替换内容，已经和兵棋没什么关系了，这种认识早就完全脱离了当代学术界对马克思主义辩证法合理形态的探索．

国内外学术界对马克思主义辩证法合理形态的探索，伴随着如何建构其科学体系以及如何理解其真实意义等相关问题研究．在国内几十年一贯的哲学原理教科书的官方表述中，往往强调唯物与唯心的对立相反，而今天的学者则强调两者在辩证法运用上的相似．人们也经常认为辩证法是“实体的逻辑”，而实际上辩证法是“关系的逻辑”．辩证法的内涵逻辑是以某种特定的关系思维而非实体思维为其解释原则的．

实体思维是指将存在预设为实体，并理解为事物的属性及其关系的最终根据和载体，以实体为前提诠释一切思维．无论是关系还是过程，都以实体载体为依托，没有了实体也就没有了关系，如此去考察社会存在作为社会关系的逻辑内涵．实体思维在兵棋中最典型的表现就是以算子（棋子）为实体性依托和根据去理解人们实际的推演过程，易于反映每一个实体模型，尤其是在复盘评估中体现为武器装备的运动和消耗和得分点的归属，于是难以进行关于作战行动及其联系的解释．

关系思维是指将存在预设为动态关系，而将存在者预设为关系的凝结物，关系具有相对于存在者而言的逻辑先在性和不可还原性，是人的认识对象及其属性生成的必要条件，也是定义任何事物的基础．关系思维在兵棋中最典型的表现是在（对抗的）命题逻辑系统中增加一个关系运算，其形式是“ 对抗Ｃ在关系Ｆ中实现 ”，如以下解释：

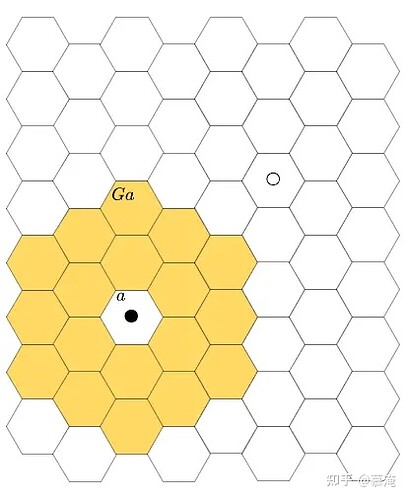
我们首先抽象掉地图（棋盘）上的对象（地形地物）及其属性（移动力消耗、防御力加成等），即给定一个由同质六边格铺满的数字空间（不含地图信息），以及一个位于ａ格的抽象的我方算子（黑色）和一个抽象的敌方算子（空心）．

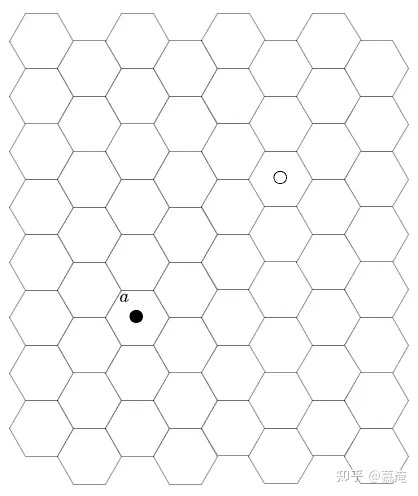
图1．给定一个由同质六边格铺满的数字空间，以及一个位于ａ格的抽象的我方算子（黑色）和一个抽象的敌方算子（空心）

我在《为什么军事家可以使用地图指挥作战？》（https://mp.weixin.qq.com/s/lUD-c74hFu6nejavesGqAA）一文中所指出的数学原因，其背后隐含着一个推论，即 算子与地图在数字空间中没有分别 ，这个推理过程不在此文中赘述，将来另行刊布．由此，我方算子的属性所构成的集合亦可记作ａ（且ａ中不含地图信息）．假定我方算子的侦察能力为２格，在ａ格（如雷达开机后）进行侦察，不能够发现敌方算子，这时候属性集合中关于信息对抗的数组要经过运算Ｆ得到Fa．

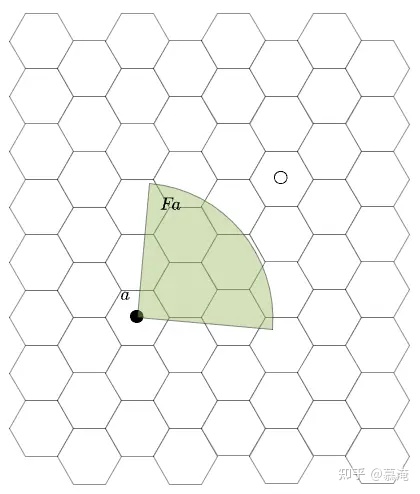
图２．关于信息对抗的数组要经过运算Ｆ得到Fa

同样，假定我方算子的火力打击距离也是２格，由于距离敌方算子４格，这个时候即使经过火力打击运算Ｇ得到Ga，也不能够打击到敌方算子．

413×507 42.8 KB

图３．经过火力打击运算Ｇ得到Ga，也不能够打击到敌方算子

于是在决策中，我们首先要进行空间对抗，通过运动接敌，我方算子机动２格距离到ｂ格，即经过这一次机动的运算ｆ得到ｂ．

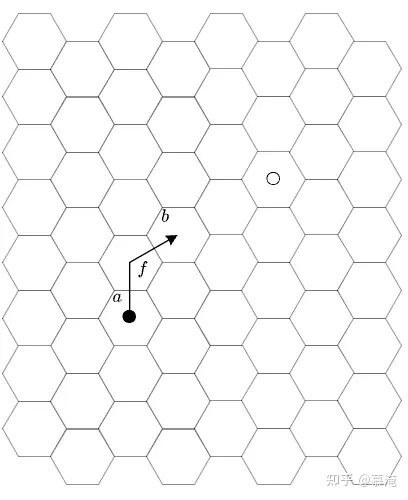
图４．由ａ经过机动的运算ｆ得到ｂ

空间对抗在敌我的空间关系中实现，这个关系也就是敌我的空间态势，我们将这个过程用交换图的形式表现，则关系就是图中的箭头ｆ：

图５．空间对抗的交换图

我方在ｂ格进行侦察能够发现敌方算子，这时候属性集合中关于信息对抗的数组要经过运算F得到Fb．

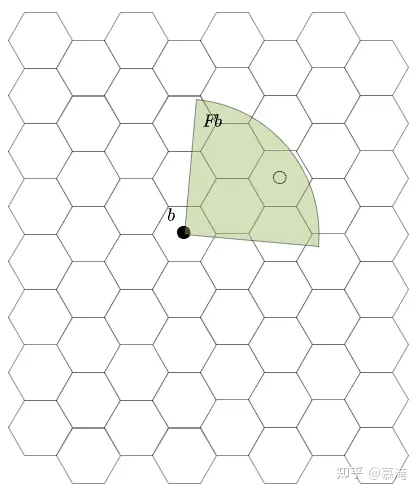
图６．在ｂ格经过运算F得到Fb

通过比较图２和图６，会发现Fa的特殊性在于无论我方雷达是否开机都得不到敌方算子的有效信息，换句话说Fa充当了在司令部检索态势信息的过程，亦表示侦察一旦发生就会刷新侦察行动发出者的情报信息，那么Fa就是初始的情报态势．由于侦察运算跟随着机动运算，所以记为Ff．侦察运算Ff将情报态势Fa映射到情报态势Fb上，信息对抗在敌我的信息关系中实现．

图７．侦察运算Ff将情报态势Fa映射到情报态势Fb上

这个时候经过火力打击运算Ｇ得到Gb，能够打击到敌方算子．

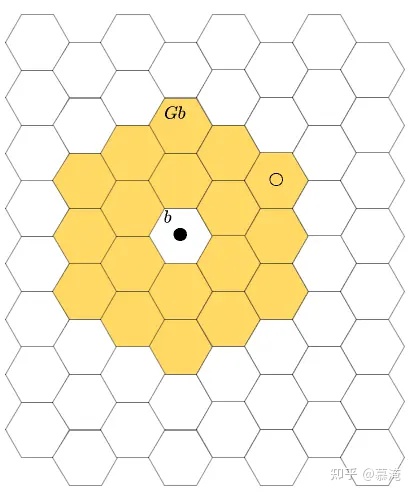
图８．经过火力打击运算Ｇ得到Gb

同样，Ga的特殊性在于无论我方是否打击都得不到敌方算子的毁伤结果，换句话说Ga就是初始的火力态势．由于火力运算跟随着机动运算，所以记为Gf．火力运算Gf将火力态势Ga映射到火力态势Gb上，Gb就是对敌方算子打击的裁决结果，火力对抗在敌我的火力关系中实现．

图９．火力运算Gf将火力态势Ga映射到火力态势Gb上

在实体思维下，兵棋推演的复盘评估表现为武器装备的运动和消耗（见图10），也就是机械地将三个交换图并列放置，割裂了空间对抗范畴、信息对抗范畴和火力对抗范畴三者之间的关系（见图11）．

720×605 32.8 KB

图10．FCSS中的复盘评估统计报表

图11．在实体思维下割裂了三个交换图的关系

在关系思维中，要求我们不仅要注意在一个对抗范畴之内的对象及其关系 （数组ａ经箭头ｆ映射到数组ｂ；数组Fa经箭头Ff 映射到数组Fb；数组Ga经箭头Gf 映射到数组Gb） ，也要照顾到一个对抗范畴之内的对象及其关系如何映射到另一个对抗范畴之内的对象及其关系 （箭头Ｆ将数组ａ映射到数组Fa上，将数组ｂ映射到数组Fb上，将箭头ｆ映射到箭头Ff 上；箭头Ｇ将数组ａ映射到数组Ga上，将数组ｂ映射到数组Gb上，将箭头f 映射到箭头Gf 上；箭头Ｈ将数组Fa映射到数组Ga上，将数组Fb映射到数组Gb上，将箭头Ff 映射到箭头Gf 上）．

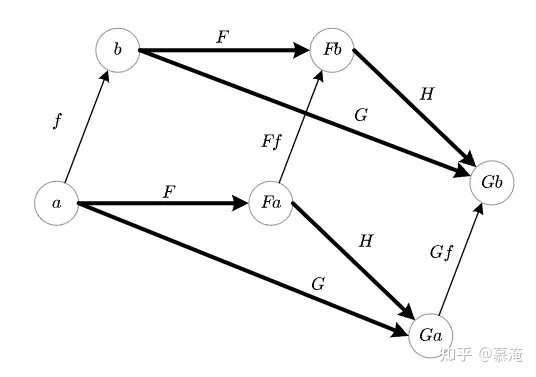
图12．一个对抗范畴之内的对象及其关系映射到另一个对抗范畴之内的对象及其关系

这是什么意思呢？其实图12从范畴论的角度解释了我方算子的战斗结构，即战斗所包含的一系列武器装备系统对抗行动的性质、数量及它们之间在目的、时间、空间上的关系，尤其重要的是，这个战斗结构符合人类推演者的主观能动性．不但情报态势与空间态势有关，火力态势也与空间态势有关，并且火力态势还与情报态势有关．这说明在这场战斗中空间对抗既服务于信息对抗，又服务于火力对抗，而信息对抗则服务于火力对抗．同时，无论是机动／侦察／战斗中哪一种对抗，都必须在构成对抗性的关系中才能实现．这已经向我们昭示，兵棋推演充分体现着马克思主义辩证法“关系的逻辑”．

在战役矛盾运动上也要注意范畴之间的映射，正如孙景伟在书中所写的一样：

（定陶战役）包含一系列兵团级的战斗、交战等作战行动．如数个阻援和反阻援战斗，还有围歼敌第３师的战斗．这些战斗之间的联系是客观存在的．首先是目的上的联系：各阻援战斗保障了歼灭敌第３师的战斗，没有阻援战斗的成功，就没有歼灭敌第３师战斗的胜利．其次是空间上的联系：各战斗之间在空间上应该有一个合理的排列．如阻援战斗应该与歼敌战斗在空间上保持一定的距离．太近了，援敌的炮火会影响歼敌战斗的实施．……第三是时间上的联系：阻援战斗应该坚持到歼敌战斗的胜利，如果做不到这一点，就会影响歼敌战斗的胜利，反之，歼敌战斗也必须在一定时间内完成任务．它持续时间越长，对阻援战斗压力就越大．……一系列作战行动之间在时间上也必须科学地排列．

这便是说，可以从阻援战斗的初始态势映射到阻援战斗的最终态势，又可以从阻援战斗的初始态势映射到歼敌战斗的初始态势，从阻援战斗的最终态势映射到歼敌战斗的最终态势，从阻援战斗的运算映射到歼敌战斗的运算．从阻援战斗范畴映射到歼敌战斗范畴，这一种映射研究的是一系列这种行动如何服务于一系列那种行动，这种服务就是战斗之间的关系．如果不研究这种服务，不研究这种关系，就不能称之为指挥科学，更谈不上指挥艺术．推演分析的研究内容就是考察不断地变换关系对实现作战目的影响．

以上研究回答了在兵棋上怎样从定性到定量地确认对抗行动及其联系，至于“量”怎么定，不是这一次的篇目就能囊括的．

4 个赞
2

所以我觉得楼主不如直接讨论抽象代数在兵棋中的应用，或者范畴论，再和算法以及兵棋软件设计方法结合起来，讨论马克思主义固然有道理并自洽，但是我还是觉得是可有可无的东西，对兵棋发展起不到什么作用，现在设计兵棋的一线设计师没什么人懂那么深刻的哲学道理的吧，大家已经有成熟的工作方式，目前并不需要很大的改变。

3

国内一线设计的专业需求，十年前是要一套兵棋就够了，今天却不行，逐渐有越来越多的需求包括提供复盘评估体系，这就等于提出了理论建设的需求，不能用以前成熟的工作方式拼凑出一个体系．

最直接的例子是上文中引用的定陶战役，复盘明确说明了目的、空间和时间上的联系，而用以前成熟的方式评估，在统计报表里只给出损耗，以及逾1000条甚至３、４千条的日志记录，如何能体现出联系，全部要依靠人脑来辨别，不单单受人的思维训练效果的制约，也是在有限的人力和时间里不能完成的任务，必须委托给计算机，这是必然的发展趋势．

现在我来告诉你为什么不能直接讨论抽象代数和算法．

第一个角度，我们所熟知的兵棋算子战斗力赋值方法，最常用的是指数法．我们不讨论它的具体步骤，而从数学本质上说，战斗力赋值是一种概率度量迭代法，基本逻辑是依据少量数据或者直觉来假定某个概率，通过数据的不断更新对概率的估算进行迭代．我们给一个算子赋上一个指数，整个过程实际上是对一系列指数分配一个权重，当赋值的推演效果不佳时，增加更高或更低的指数的权重．上一篇叶含不理解为什么要提概率扭曲函数π(p)，这里就是一个应用．比如算子可以赋值3／5／7／10中的一个，权重倾向于5或7，可以用概率表示为10%、40%、40%、10%，推演检验之后发现权重倾向于更高一些，于是概率就变成2%、8%、40%、50%．我们从这个具体实例中抽出身来，在兵棋设计当中有很多方法要涉及到概率理论，并且推演当中的诸多评估也要用到概率，这就必须在概率测度上扩展出哪些条件是可测的，哪些是不可测的，然后在概率空间中才有统一的变换规则．

第二个角度，兵棋游戏中的战斗力计算逐渐向军事运筹倾斜，而解放军对战斗力计算的研究一直是重大理论热点．我在此不列举我知道的理论名录，这些研究高度总结了应用数学层面的经验公式．然而其中有部分人误解了数学和物理学的研究范式，将雷达图当作是坐标系来研究，把不能用向量处理的东西当作向量（《B4M人机对战及其蓝方先手首轮推演分析》word文档第４页注释７）．实际上，只有当向量是一种独立于坐标系选取的客观物理量，并且满足与坐标变换相匹配的变化规律时，为军事研究建立一个坐标系同时研究向量或张量变换才有数学意义，才能满足群、域等数学运算理论．换句话说，以计算机兵棋来看，推演数据的矩阵变换要求对矩阵本身的数学对象进行辨析．此外还有战斗力量纲的问题，指数法的根源要求对战场或试验场数据进行统一的量纲规定，一旦没有统一的物理含义，就要对运算合法性进行辨析．弄清楚兵棋推演数据中一种特定数组的群理论以后，与之同构的其他特定数组就能进行相同的运算．而难以确定代数结构的数组则可以通过范畴论找到函子，找到等价范畴．

第三个角度， 在兵棋推演中算子代表对阵双方的兵力兵器，用来表示一定的单位或事件，在手工推演中算子通常包括单位算子和注记算子两大类，而在计算机推演中只需要考察单位算子的形式．成熟的方法依据的是实体思维，在上文中已经有所表述．实体思维在设计算子或者武器装备的时候，必然会陷入概念重叠的问题，在我经历过的项目工程化和装备概念体系构建工作中，始终绕不开．这个问题也在学术界出现，比如《武器装备系统概论》提出"信息作战武器"这个概念，实施信息获取的侦察探测系统和告警系统，实施信息传递的通信网络装备，实施打击破坏的干扰装备、干扰弹药、反辐射武器和定向能武器，实施计算机网络攻击的网络武器，都包括在其中，但在军语中没有这个概念。如果兵棋算子代表的单位实体包含着装备、平台、武器、弹药、传感器和其他设备等六类，那么蠕虫病毒应该归在哪一类？侦察和干扰是两种功能、两种规则，放到一体机里，归于哪一类？如果说实际工作可以把理论拆开使用，那么实际工作可不可以整理成工作理论，在这个理论里还是绕不开实体思维必然携带的缺陷．

这些角度促使兵棋设计师必须站在更高层次上对兵棋再一次进行抽象，首先解决相容性问题，这就是为什么不能直接讨论抽象代数和算法．

当提问“为什么军事家可以使用地图指挥作战”时，我们可以找到一把钥匙，在地图上识图标图是一种高级抽象，图上的部队记号、行动箭头和地形地物的记号是同质的（即物质的均匀性无剧烈差别）．换句话说，（忽略碳粒后）在一张纸上不会再有第二个实体，部队记号、行动箭头和地形地物的记号都不是别的什么实体，它们只是人为对纸张进行了分化以及叠层，为的是体现分化之间的关系．因此必然有一种数学语言可以描述这种算子和地图没有分别的这件事．于是从这一点出发必须取消实体的观念，转而建立关系的观念，这就自然而然导向了辩证法．

4

感谢回复，我只是业余爱好者，不像你这样做专业研究，我感觉这是一个很厉害的事情，不知道国外学界有什么类似的研究不。
但是我不理解为什么要导向辩证法，你说了地图作为实体是人为对纸张进行分化和叠层，导出后文的数学语言可以描述这种算子和地图没有分别的事情。
问题是抽象出算子，标记啥的东西，是一个非常成熟，广泛使用的事情，人类目前还没有找到啥更好的方式，因为兵棋这个东西最终还是要让大多数人能容易理解的。你说要取消实体，建立更抽象的数学描述有什么意义？复盘评估我相信国外兵棋界也有很成熟的思路了吧？
或者说你想从底层重构兵棋复盘或设计的框架，至于怎么让普通人理解是后话，但是你觉得这个事情很重要，所以要先讨论这个？

5

我想了两天，你的这个意见我还是应当考虑展开陈述的。为什么先讲这个，其实是项目工程化的一个扩展的隐含的要求。在一线设计中，我们对比和吸收了兰德的一些方法（比如德尔菲法）到从定性到定量的综合集成研讨厅方法中。综合集成研讨厅方法有一个不严谨表述下的缺陷，就是这套方法并没有接受过最严格的革命战争的检验，它不是从革命战争中提出的工作方法，但形式上是靠近的，因此必须在革命战争工作-综合集成研讨厅方法-兵棋三者的贯通中确立具有中国特色的方法和理论。打一个通俗的比方，《大决战》拍出了一定程度的工作状态，想象一下假如战略层和战役层都在用计算机兵棋，应当是怎样工作的？综合集成研讨厅方法能容纳组织上的讨论过程，而在兵棋推演上尚缺少辩证法的推演数据运算理论综述。这是一方面，另一方面从更加普遍的层面上看，为什么要导向辩证法，不外乎是基于条件事件代数的概率逻辑推理问题（核心是通过建立布尔型条件事件代数，扩充概率空间和概率测度来解决条件推理问题），推演数据中蕴含的概率逻辑关系（概率因果关系）可以描述各属性变量间的相互依赖及依赖关系的不确定性，利用推演数据的概率因果关系可以找出变化规律。而在钱学森的描述中，这两个方面原本就是紧密结合的，辩证唯物主义的辩证逻辑是系统科学理论不可缺少的逻辑方法和工具。

如果再扩展来说，手工兵棋是基于规则的推理系统，属于较低层次的数据处理方法，包含三个组成部分，规则库、证据库和推理引擎，是一个if-then语句，用概率描述可信度，进而得到这种可信度的其他形如if-then的结论。但是手工兵棋向计算机兵棋过渡以后，必然要发展到传感器管理、态势评估和威胁估计等较高层次的数据融合阶段，这就需要布尔代数的除法运算。C3I系统要求容纳更高阶的推理，也就是基于事件条件性和规则推理的数据融合方法，在国外军事领域已经做出了发展，国内只是相对缓慢，比较热烈的是随机集理论在数据融合上的应用，还有西北工业大学何华灿教授从泛逻辑学出发讨论结合概率描述的不确定性推理逻辑规律。 还有一批研究者基于辩证唯物主义研究具有普适性的人工智能基础理论，比如数学基础和矛盾转化等方面。从某种意义上说，我写下这些想法是为了从一个更加自洽和统一的数学语言上去整合这些研究，找到一个新的评估方法，以此为目的设计兵棋。

6

我认为CMO的设计已经十分完美，可以参考CMO的设计进行制造。

7

CMO固然优秀，但我们也要看到它的局限性。

所谓战斗是敌对双方为完成各自的作战任务，运用武器装备系统所进行的有组织的激烈的暴力对抗行动。CMO和墨子，是典型的围绕武器装备系统的资源运筹对抗，可以细化到操作武器装备系统的战斗参数。 在编制我们所认为的战役级想定时，仍然围绕着武器装备系统的对抗资源运筹的操作。铺开了是战役空间和战役军团的体量，真正操作的时候，玩家都要一级一级下放成为战术指挥员，去操作每一个战术兵团的算子，甚至是分队的算子，这种操作思维是CMO本质上属于围绕武器装备系统的资源运筹对抗却包揽了战役想定的原因之一。

换句话说，CMO和墨子的战役想定推演过程，都不能照顾到一系列作战行动及其之间的联系，不能对此进行决策和评估，而这才是战役推演所要探究的核心内容。

2 个赞
8

同意，但CMO已经基本涵盖了本人需求的战术级运用了。

9

有一个问题可以请教一下吗。
您的B4M推演中引用的这段：
这意味着，存在一种“兵棋的数学原理”，它必须能够完整地说明兵棋推演的代数运算合理性。
西方经济学都是建立在“理性人”“市场”假设这些公设上的，请问兵棋学能否建立在公设上？

10

如果你了解了战役矛盾运动规律，那么兵棋设计的目标就会自然朝向实现作战结构的量化过程，目前我所在的部门对这个问题已经有了很好的策略性进展。对于战略和战役所关注的问题，仅仅依靠代数运算合理性是不能够解决的，在军事科学中也始终没能解决，实际上涉及的根本问题是军事辩证法要区分可计算性和不可计算性，哪些明确不能用包含兵棋技术的计算机工程来实现，这是一个哲学问题+软件工程问题。可变模糊集、泛系哲学和广谱哲学走的是公设化道路，但我不建议做同样的事情，除非你有足够的精力和勇气涉足唯物辩证法和辩证逻辑的领域。以目前我们的经验来看，这并不是一个当前优先的任务。数学形式逻辑要有，但不要在设计经验以外另行搭建理论大厦。当初我提到“兵棋的数学原理”，是希望能够在军事科学的作战计算模型中找到一个桥梁，映射到兵棋规则的计算模型上。而从现在的结论上看，为了要找到支撑作战结构筹划的结构方程，似乎存在另一条路，目前不需要公设化。

11

Ff 是一个运算还是应该理解为 Ff = F ○ f ? 是想表达先机动再侦查的意思？那这样的初始状态写成 a 是不是更合理，亦或是有别的含义？我认为这里把 Ff 改成 f 才容易理解。后面 Gf 同理。

这有点画靶射箭了。足球比赛最开始统计传球、射门、犯规这些一级指标，后来发现控球、跑动重要又开始广泛统计，再后来给球员机器打分，不久前才出现依赖更复杂模型的xG. 把类似的逻辑拿过来就是足球的统计数据割裂了场上各个阶段之间的关系，但这是只关注这些指标的结果，不是原因。效率分析依赖更深的数据挖掘工作。兵棋复盘使用的统计指标在我看来也类似足球，因为最终只有比分（推演结果）有用，找到不同指标之间的联系是次要的。

两个疑惑。其一是，如果定义了运算 F 与 G, 那么运算 H 的含义是？实现 H 运算是不是必须使用 F^{-1} ○ G ? 你或许想表达 Fa 与 Ga 存在关联，但 H 似乎不能既离开 F 与 G 定义又满足图示关系，这样容易误导读者认为 Fa 与 Ga 之间存在简单的转换关系。
其二是此前提到的在 f 上的记号的问题。如果用 f 描述，那么把 a, Fa, Ga 看作一个整体，b, Fb, Gb 看作另一个整体，这样只需一个 f 运算就可以实现两个整体之间的映射。这样是否更直观更合理一些？

全文在讨论时间关系上过于含糊了。兵棋在时间上的演进是自然的，但是一抽象就出问题了。首先，时间状态变化是否存在可逆关系，至少我看不出对时间作逆运算有什么实际依据。其次，如果抽象兵棋模型，在某个状态 a 上的所有运算都可能含有时间变化，对 a 作 F, G 运算时，时间演进会导致得到某个 Fa’, Ga’‘, 这样 H 的关系可能就不存在了，因为 Fa’ 不能回到 a. 最后，在你给的模型当中，只有运算 f 隐含了时间变化，这样 f 就与 F, G 存在根本区别，即 f （例如是机动）最多在空间中可逆，而不在时间中可逆，导致 b 不能回到 a. 你的关系模型中应当怎样表达时间上的关系？可以忽视时间关系吗？

我的建议是先别考虑怎么定量的问题，先把时间关系加进你的模型里，以及考虑运算 H 的表达方式，看看是不是还适合使用关系的模型描述。a, Fa, Ga 都可能不会静止不动，如果不做 f 操作，怎么定义某一个对象。先考虑时间和空间上的状态转移，再考虑关系，也许合理一些。

12

提的这些问题真是太好了！

第一个问题，这篇稿子是从笔记中摘录的，我忘记抄进约定记号的含义了。跟随记号○我省略了，所以Ff就是F○f，f(a)的括号也省略成了fa。我是顺手用了小写字母abfgh和大写字母FGH，ab表取值，fgh表三种对抗操作，FGH表对抗之间的映射操作。如果规整一点，应该是同音字母大写表操作，小写表取值，后续研究会统一改写。

“找到不同指标之间的联系是次要的”，这种看法不对，无论是我军军事理论、军事辩证法还是根本的唯物辩证法，都强调要找到联系，并且是指挥员主要的工作。刚好我写了另外一篇，恰巧也类比了足球，请移步 请问有没有1款战略游戏可以在战略层面指挥战斗（就像钢铁之师2的将军模式那样，谢谢）？ - 知乎

找到联系的重要性，以围歼战斗和阻援战斗为例。从目的上说，阻援战斗行动与围歼战斗行动的关系很明确，就是解除内线作战压力，因此阻援战斗应以围歼战斗的胜利为胜利，在时间上应该坚持到围歼战斗的结束，在空间上应与其保持安全距离，两者可以从行动的时限和区域上加以确定，不让阻援战斗当面之敌影响围歼战斗行动。只有找到联系，才能进行战役布势，才能根据战场变化改变行动。

很多人推演的时候可能偶尔会注意到这些联系，但是决策和评估如果不以此为出发点，那么推演结果其实是无用的。我们关心的是前置行动的状态改变是否对后续行动的状态改变产生影响，因为前置行动可能无法达成行动目的，但是后续行动并不一定会因此而取消。比如“阻援部队展开行动”虽然在前，但是有可能由于意外情况使得部队没有顺利进入阵地便仓促进入到阻援战斗阶段，那么当“阻援兵力进入阵地”这个条件发生改变时，对“解除内线作战压力”的影响有多大，这是我们实际关心的问题。

两个疑惑，如果你稍微了解一下数学的范畴论，应该大致能理解我的意图。这一段问题我暂且不详细解答了，实际上在撰写这篇文章时，我仍坚持着用逻辑和代数方程的标准数学语言来解决作战结构的量化。我走得比文章里略微深入一些，也就看到了标准的命题逻辑和概率演算的局限性，目前已经使用新的数学工具了。纳入范畴论的探索过于前沿及抽象，不适合作为当前优先的任务。应该回到推演本身。

时间关系的问题，从一开始我确立要分析行动及其之间的联系，就已经隐含了时变因素。在新的模型中使用因果关系来表达推演的次序关系。扬弃代数结构模型最重要的原因是抽象的推演离开了具体的推演，始终就要面对你提的这些问题。

13

说它次要是因为我认为保证应用层面的兵棋能得到可靠推演结果是第一位的，在此基础上才可能发现进一步的联系，不然兵棋提供的决策帮助就变得可疑，在此之上评价指挥得失也缺少实际应用价值。类比足球来说，就是先关注比分（或者现在认为xG更科学一些），再关注其它数据是否反映教练的执教水平或者球员表现等等。
另一方面来说，找到这样具体的联系很困难。我不太确定理论上是不是存在这样一种普适的指标去评价。在具体的模型里，比如2人德州扑克这样相似且具体的模型下，有没有一个让人满意的指标可以评估选手的表现（除了收益水平，这是最终结果）。至于像足球这样更复杂的模型里，机器打分至今也不是非常靠谱。

这里已并非我所提到的不同指标之间的联系了，而是回到了模型准确性的问题上。前后事件之间的影响应该通过预先设计好模型从而推演得出，还是首先发现相互影响的关系才能制定准确的模型呢？或者说，用谁去检验谁（或者相互检验）的问题。
我对业内了解非常有限，不知道行业里用什么方式保证模型可靠，我也长期好奇除了专家意见之外什么可以作为可靠的模型建立出发点。
最后，我不懂模型设计有没有所谓哲学指导，也不会考虑从这里出发去论证模型可靠性。就像二分类问题用准确率、召回率、auc这些指标一样，实在的验证才是最有说服力的 :slight_smile:

14

首先你这个可靠是怎么定义的，如果按照军事理论，那么可靠就是军事理论教材里的标准。所以推演结果如果不符合这一种标准的认识，那么推演结果就完全无用了。所以你的回答关于发现联系和结果可靠是不是本末倒置了？

你不确定是否存在这样的指标，是因为市面上所有的兵棋都不是按照这样的理论研制的，我们要提倡这样一种指标，也要研究这种指标。你可以查一些本体论ontology的资料，这是背后的哲学指导。