舰操图基础教程
作者:白幢
(1):本体及用途
(一)算尺(Slide Rule)
在介绍什么是舰操图之前,首先介绍一种计算工具算尺(Slide rule),舰操图就是算尺的一种,但是专用于航海或航空领域的对航向、方位、速度进行快速计算的数学工具。
以下是历史上(最主要是二战前)用作军事目的算尺:
REF K&E M4 Graphical Firing Table Slide Rule - 1943
Fesenthal (Dalton) Dead Reckoning Computer (c1940-1944) Type E6B****U.S. Army Version WWII
US Navy Calculator For Vertical Aerial Photography, MIL-C-19729
REF Japanese Gunnery Correction Slide Rule
算尺,其本质是一种对数计算尺,一种模拟计算机(Analog computer),或者说小型的机械计算机(当然其不同于当时已经出现的由黄铜、钢铁、标尺和齿轮制成的机械计算机),通常由几个互相锁定的有刻度的长条和一个滑动窗口(称为游标)组成。在 1970 年代之前使用广泛,之后被电子计算器所取代。
其实在当时的海战中已经大量运用到了机械计算机,比如潜艇上的鱼雷数据计算机
(TDC,Torpedo Data Computer),比如美军轰炸机上的诺顿轰炸机瞄准器和火力控制系统,有些器件甚至直到二战结束数十年后仍未退役,其中一个例子就是由美国海军开发的马克 一号火力控制系统,各式驱逐舰到战列舰都看得到它的影子。
诺顿轰炸机瞄准器
二次大战之前,当时的最精密的科技就是机械式和电动式的模拟计算机,也被认为是前途光明的计算机趋势。但是跟现代的数字电脑比起来,模拟计算机相当不具弹性,必须手动装配设置参数(重新改编程序)才能处理下一个待解问题,不过早期的数字电脑能力有限, 无法解决太过复杂的问题,所以当时的模拟计算机还是占有优势。直到数字电脑越来越快, 拥有越来越强的记忆能力(RAM)之后,模拟计算机就迅速被淘汰了。
(二)火控系统(Fire Control System)
对海战有一定了解的朋友应该知道听说过舰船上的火控系统(Fire control system), 它们控制射击武器自动实施瞄准与发射的装备的总称。火控系统是由许多组件结合而称的系统,主要包含火力控制计算机(gun data computer),辅助导引装置(director,又译为指挥仪)和雷达(radar)。火控系统执行的任务与人类炮手相同,但可以更快并准确的完成任务。
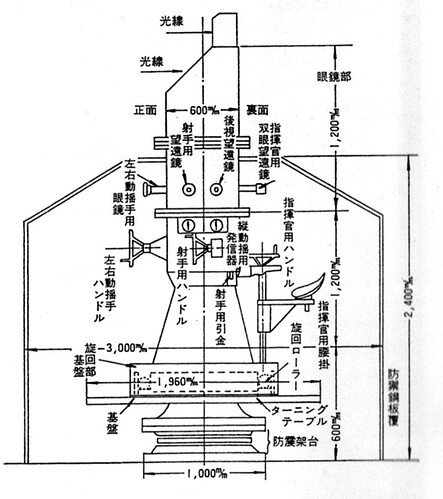
美国在太平洋战场上的敌人日本人的舰船上也装备了火控系统(日文为**「射撃指揮装 置」**),比如大和号上主炮和副炮所装备的九八式射撃指揮装置。
九八式射撃指揮装置
而一个完整的射撃指揮装置还可以细分为以下部分:
方位盤 (高射機):瞄准目标并获得当前方位和高度。(相当于 Director )
射撃盤(高射射撃盤):求解目标的未来位置并计算射击参数。(相当于Rangekeeper )
照準器:通过设定参数和瞄准目标,找到所需的射击参数(砲側照準器、環型照準 器等也属于此,但必须与照準望遠鏡区分开)。(相当于 Gun Sight)
測的盤:分析目标的运动轨迹(目标运动矢量)。(相当于 Tracking System)
測距儀:获得目标的当前距离。(相当于 Range Finder)
電波探信儀:获得目标的当前的距离和方位。除此之外,一些用于也可以获得目标 当前的高度。(相当于 Radar、Fire Control (FC) Radar )
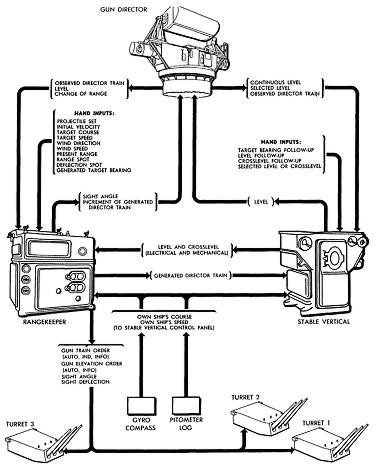
美国的标准火控系统的构成(以Mk-38为例)
对二战时期的火控系统感兴趣的可以看我的另一篇文章介绍文章《海军火力与技术》(推 书贴)。
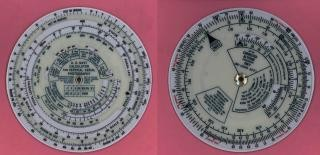
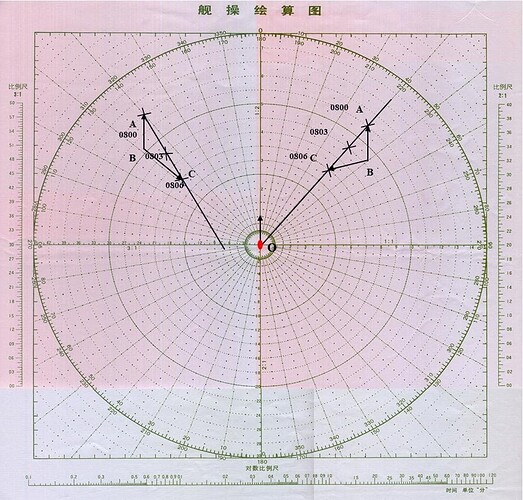
而舰操图就是主要辅助判定航向,航速,方位的一种作图工具。 下图为日本的九八式運動盤。
九八式運動盤(Type 98 Maneuvering Board or Maneuvering Slide Rule)
"九八式"表示它是在公元 1938 年(日本皇紀或神武历 2598 年)设计制作的。
九八式運動盤是一种极坐标测量工具,用于计算两艘移动船只(或物体)之间航迹和距离数据,通过方位盤和射撃盤将角度数据输入火控系统,其专为大和级战列舰(大和号和武藏号)而设计,也可以作为较小的枪炮的计算工具,一般这些枪炮没有连接到主炮的火控系统上。同时也可用于舰炮对海岸或岸炮对舰船的射击。该舰操盘的另一个特点是其旋转拨盘可用于进行航向校正和风漂流(wind drift)的计算。如果战列舰大和号或航空母舰上有飞机起飞的话,它也可以用来计算出最佳航向。潜艇也可以使用类似的设备来计算拦截航线。
其实九八式運動盤的设计正是模仿盟军的舰操图(Maneuvering Board)。盟军的舰操图设计于 1920 年,至今仍在使用着。
1943 年 12 月 23 日,所罗门群岛的行动中,蒙彼利埃号航母(CL-57)上的舰操图作业。
(三)舰操图
舰操图(Maneuvering Board)是用于解决相对运动问题的极坐标绘图板
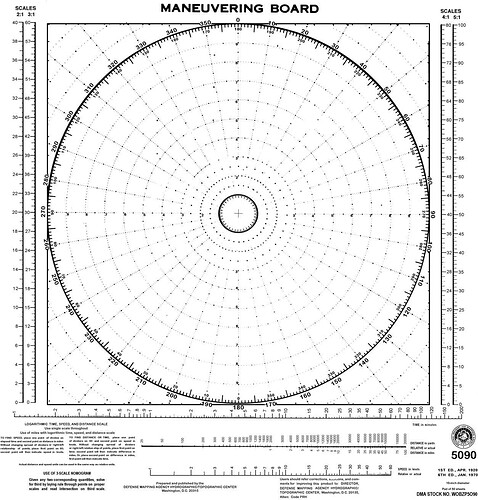
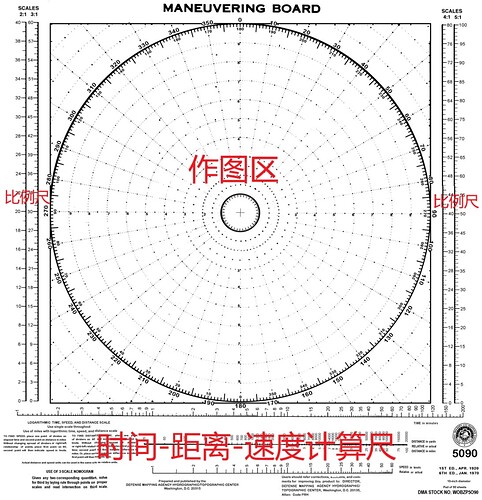
(polar-coordinate plotting sheet)。一般白底印制,有 10 英寸和 20 英寸两种尺寸,分别为 5090 和 5091。舰操图 5090,如下图所示,主要由 10 个等间距的同心圆和 36 个中心轴线组成,轴线以 10°间隔虚线印刷。除了最小的内圆和和最大的外圆之外,其他同心圆也是点状绘制。全图直径为 10 英寸。
同时每个同心圆又细分 5°的间隔刻度。
以 10°为间隔在外圆标记方位刻度。标记为 0°的轴线也标记为 180°。
底部是诺模图,一组对数的时间-速度-距离刻度尺(time-speed-distance scale)及其使用说明打印在底部,用于计算速度,距离和时间。左边缘有两个垂直刻度(2:1 和 3: 1),右边缘有两个垂直刻度(4:1 和 5:1),称为速度/距离刻度尺(speed/distance scales)。
除尺寸外,图表 5090 与图表 5091 完全相同。
舰操图(Maneuvering Board)
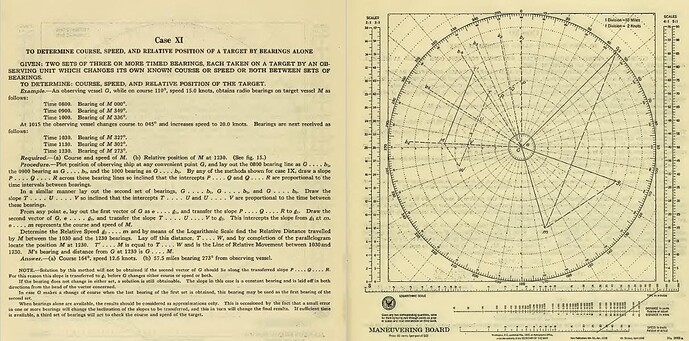
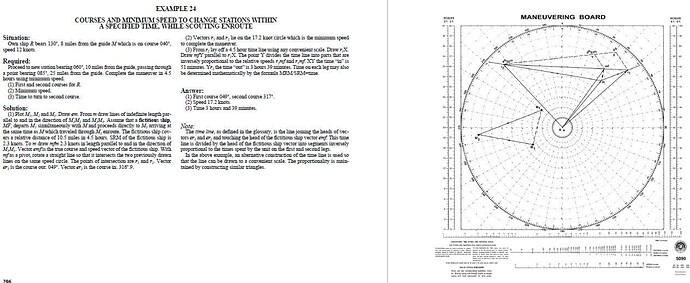
在美国在二战开始前已经广泛使用舰操图作为工具。下图分别是是 1941 年和 2001 年美国政府出版的 Maneuvering Board Manual 中的一道题:
只通过目标的方位确定其航向、速度和相对位置。
1941 Maneuvering Board Manual
2001 Maneuvering Board Manual
一般来说,战舰在航行时,位于战舰 CIC(Combat Information Center)的人员会使用各种设备——雷达,雷达中继器,NTDS(Navy Tactical Data System),DRT(Dead Reckoning Tracer),水面目标测绘板(surface plot)和舰操图——获取侦察范围内所有目标的信息,即航向,速度和 CPA(closest point of approach)等。
舰操图正是用于确定本船和接触目标之间的相对运动。由于相对运动对于本船的安全性很重要,CIC 的人员必须能够解决各种类型的舰操图使用问题。
接下来我们将来讨论一下舰操图的使用,从最基本的所需知识到实际的运用,然后进入 更高级的问题。
(2):基础知识与概念
序言
上一章介绍了舰操图的本体与用途,这一节,我们将讨论一下使用舰操图的基础知识与概念。
舰操图(Maneuvering Board)的提法更偏向于军事领域,这种图上作业方式在民间航海领域一般被称为雷达标绘(Radar Plotting),主要用于航海途中解决一些问题,比如:
(1)是否存在碰撞问题
(2)采取避让措施
(3)求解恢复原航线的时机
雷达标绘纸
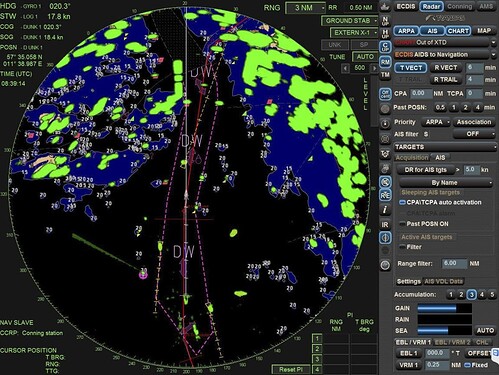
作为一种人工标绘方式在现代航海中由于速度较慢、误差较大(取决于标绘工具的精细程度)等问题而显得不合时宜,取而代之的便是计算机操控的自动雷达标绘仪(Automatic radar plotting aid,简称ARPA),一种能自动跟踪、计算和显示选定目标的航向和速度,显示碰撞威胁并能预测避让结果的雷达系统。
ARPA
当然这些并不在本文的讨论范围内,接下来是介绍一些航海的基本知识与概念。
(一)基本概念
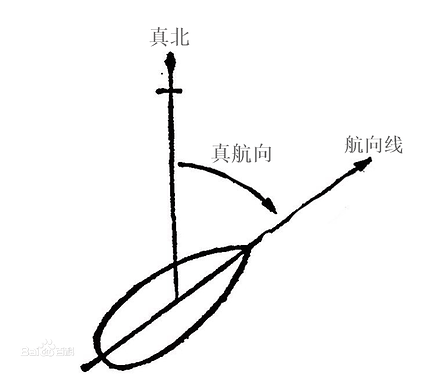
真航向(True Course,简称TC):
指的是船舶航行时,真北线与船首线之间的夹角。真航向以真北线为基准,顺时针量至船首线。
度量方法:以真北线为000°,顺时针方向为000°到360°,三位数表示。
真航向
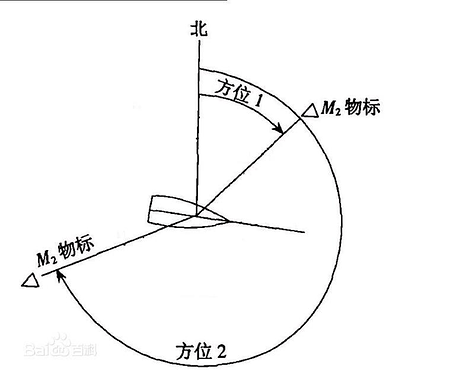
真方位 (True bearing,简称TB):
在测者地面真地平平面上,自正北方向线顺时针方向计量到物标方位线的角度。
如下图中的方位1和方位2。
真方位
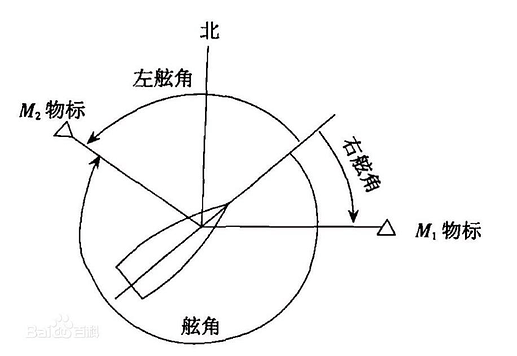
相对方位(Relative Bearing,又译为舷角,简称Q):
指航向线与物标方位线之间的夹角。
又细分为:
1)以360°划分的圆周舷角
它是以航向线为基准,顺时针量至物标方位线,范围为0°~360°。
2)以180°划分的左右舷角
它同样是以航向线为基准,向左或向右量至物标方位线,范围为0°-180°。度量时必须标明左、右舷角,向左度量的称左舷角(Q左),向右度量的称右舷角(Q右)。若左舷角为90°时称左正横,右舷角为90°时称右正横。
相对方位或舷角
航向、方位和舷角的换算关系:
方位=航向舷角(左舷角-,右舷角+)
由于航向、方位的范围在0°~360°,计算航向、方位的结果如得负值则应该加上360°,如大于360°,则应将计算结果减去360°。
航向、方位和舷角换算
(二)相对运动(Relative Motion)
在宇宙中,没有绝对的静止。
某一个物体的实际或真实运动通常根据其相对于地球的运动方向和速度来描述。如果物体是船,则根据真实航向和速度来描述其运动状态。物体的运动也可以根据其运动方向和相对于另一物体的运动速率来定义。船舶间的相对运动,或一艘船相对于另一艘船的运动的运动,是根据相对运动方向(Direction of Relative Movement,简称DRM)和相对运动速度(Speed of Relative Movement,简称SRM)来定义的。每种形式的运动可以由矢量描绘,即一段表示方向和运动速率的线段。
在进一步讨论运动矢量及其应用之前,先看一下两艘船之间相对运动的示例。
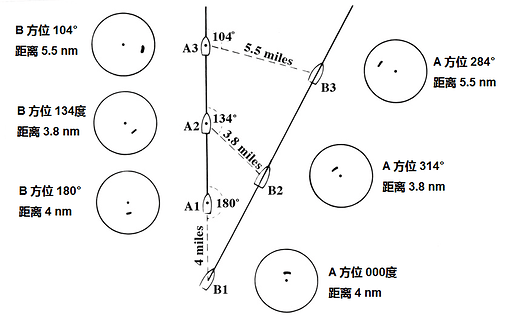
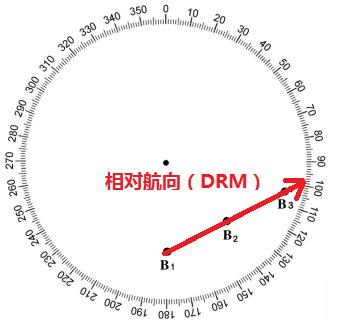
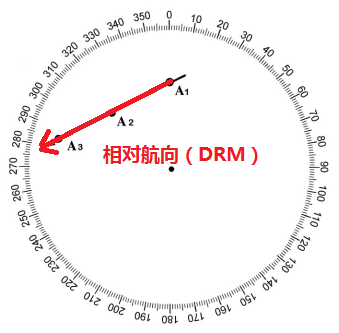
在下图中,在地理位置A1处的A船,真实航向000°航速15节的情况下,最初在方位180°的4英里处观察到B船。
当A船从地理位置A1运动到A3时,B船的方位和距离也发生变化。B船相对于A船的位置变化在对应于船舶A和B的地理位置的连续PPI表示中示出。同样地,船舶B,在地理位置B1,在真正航向026°,22节的情况下,最初观察到船舶A PPI轴承000°4英里。当船B从地理位置B1前进到B3时,船舶A的方位和距离发生变化。船舶A相对于船舶B的位置变化在对应于船舶A和B的地理位置的连续PPI表示中示出。
两船之间的相对运动
如果A船上的雷达观测员绘制了B船相对于本船PPI上的连续位置,他将得到B船运动航迹的相对运动绘图(Relative Motion Plot),如下图所示。
B船相对于A船的运动航迹
同时,如果B船上的雷达观测者绘制了A船相对于本船PPI上的连续位置,他将得到如下图所示的相对运动绘图。
A船相对于B船的运动航迹
此时,A船上的雷达观测员将确定B船的相对运动方向(Direction of Relative Movement,简称DRM)为064°,而B船上的雷达观测器将确定A船的DRM为244°。
但是,每个PPI上的相对运动图无法表示目标船只的各运动要素(包括真实航向和航速)。
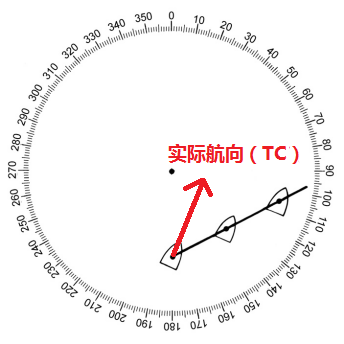
下图是B船的实际航向。
B船的实际航向(actual heading)
此时,对于任何雷达观测者来说,要确定另一艘船的真实航向和速度,就需要使用相对和真实矢量来进行求解。
(三)矢量
一般,物体的运动速度是以矢量的形式表示的。矢量是具有长度和方向的量,并且以箭头表示其方向。在舰操图中,矢量箭头用于指示船舶的航向。该有向线段的长度用于表示船舶的速度。
描绘本船真实运动的真实速度矢量称为本船真运动(航向-速度)矢量; 描绘其他船舶真实运动的真实速度矢量称为其他船真运动(航向-速度)矢量; 描述本船与另一艘船之间的相对航向(DRM)和相对速度(SRM)的矢量,即相对运动矢量(DRM-SRM)。
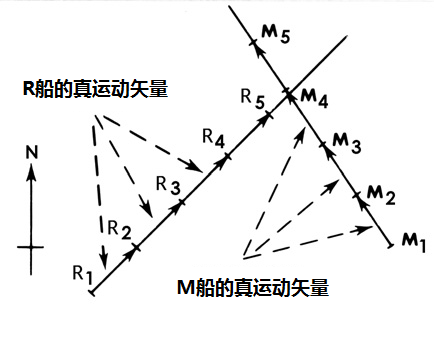
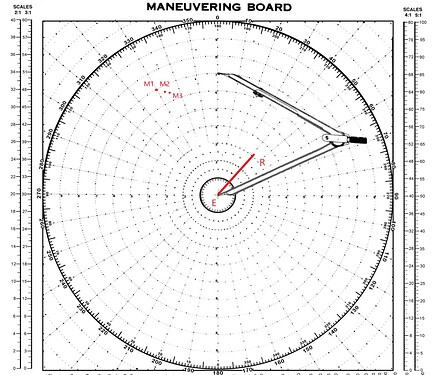
下图显示了两艘船R和M相对于地球的运动矢量,即真运动矢量。该图中R从R1运动到R5,M从M1运动到M5。
真运动矢量
船舶R在路线045°上以恒定速度行进通过连续位置R1,R2,R3,R4 …以相等的时间间隔表示出来。 因此,连接连续位置的线段表示其相对于地球的运动方向和速度。 因此它们是真运动矢量(航向-速度)。 同样,对于航向为325°的船舶M,以相等的时间间隔标示出来的线段表示船舶M的真运动矢量(航向-速度)。
但是正如前文所说,很多时候我们只知道本船的真运动矢量以及他船的相对运动矢量。
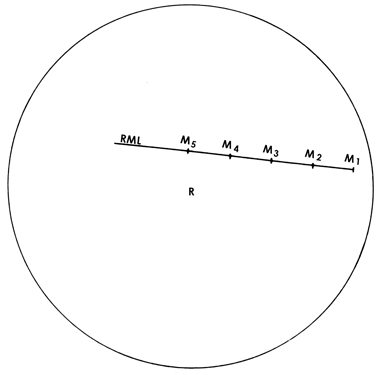
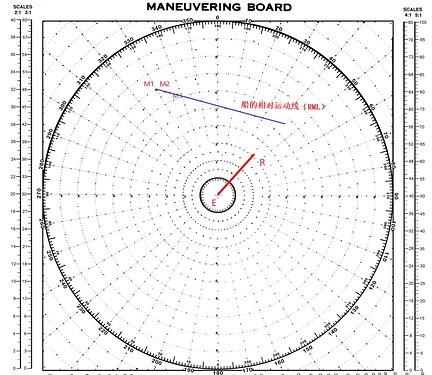
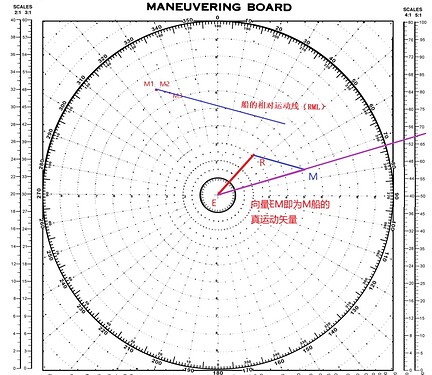
在这种情况下,我们可以通过在本船R上的雷达PPI上的船M的连续位置图(见下图),绘制出M的相对运动线(RML),而每经过相同时间间隔的线段即是M的相对运动矢量(DRM-SRM),尽管未示出箭头。
M船的相对运动线(RML)
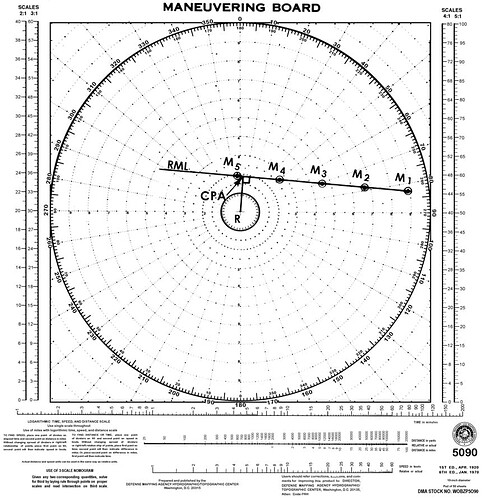
这里其实可以看出来,舰操图的本质就是在复原PPI图显示情况的基础上,通过尺规作图计算的工具(见下图)。舰操图的中心对应于PPI的中心。
舰操图
与PPI图一样,以本船R中心点为固定点。同时下图也标示出了R与M的最接近点(closest point of approach,简称CPA)。 CPA代表了一艘船与另一艘船在航行中最接近时的位置。求解CPA也是舰操图的主要用途之一,会在后文详细论述。
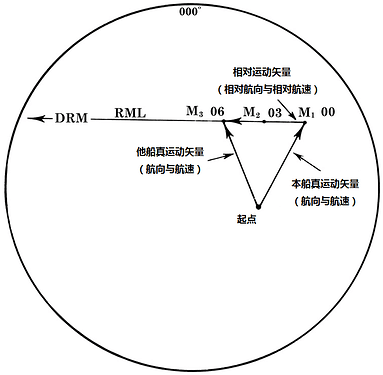
PPI上的矢量三角
舰操图的使用的最普遍问题是确定另一艘船舶的真实运动(真实航向和速度),即已知本船R的真运动矢量和船M相对于本船的相对运动矢量,求解M船的真运动矢量。
矢量运算正是应用于此,特别值得注意的是注意矢量的方向性。具体的矢量计算公式如下:
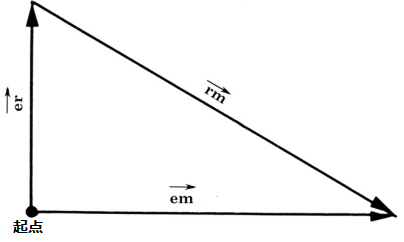
矢量三角
其中:em 是他船真运动矢量 (航向-速度);er 是本船真运动矢量 (航向-速度) ;rm 是相对运动矢量 (DRM-SRM)
em = er + rm
er = em - rm
rm = em - er
矢量运算符合平行四边形法则和三角形法则,属于基础数学知识,在此不详细论述。
(3):操作步骤与实例
(一)序言
经过前两章的介绍,想必,你已经急不可耐地想进行一下实际操作。现在正式开始舰操图使用教学。
(二)舰操图图例
首先我们来看一下舰操图的整体。
舰操图5090版,中间区域为作图区,两边为比例尺,底下是时间-距离-速度计算尺。
时间-距离-速度计算尺是一个对数计算工具,每一个刻度都可以通过:
距离= 速度 x时间
这一关系式中另外2个数据得出。
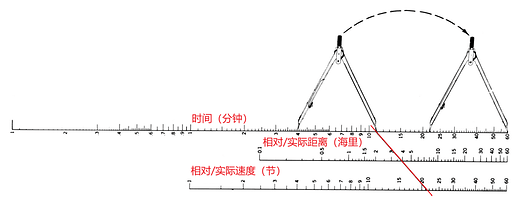
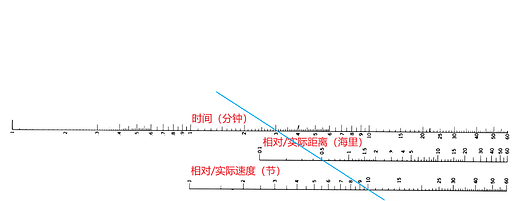
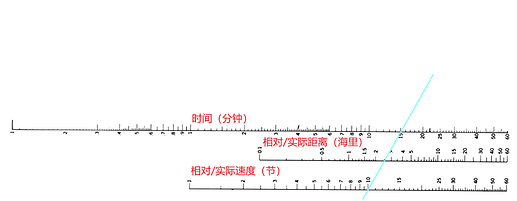
下图中演示了,在距离为4海里,时间为11分钟时的航速数据。
使用方法非常简单,只要确定3个数据中的2个,连线之后在位置数据标尺上的交点即为第3个数据。
时间-距离-速度计算尺
(三)操作步骤与实例
工具准备:
舰操图
铅笔、尺规
操作步骤:
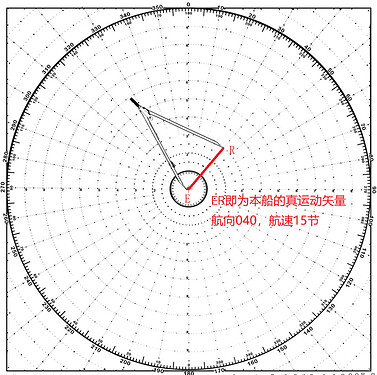
首先确定本船(E)的信息:真航向040,真实航速15节
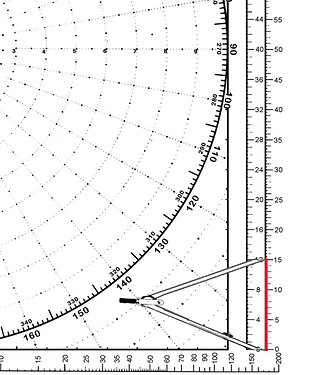
①使用圆规,在5:1的比列尺上取15,即为此时的航速15节。
②然后,用直尺以舰操图中心点为起点E(本船位置),在方位040上作出本船的真运动矢量(航向040-航速15节),即图中的矢量ER
③接着在作图区表示出目标船的的至少3个方位点(相对方位),每一个点间隔相同,本例间隔取3分钟。此时目标船的方位为330,距离本船7海里(可使用1:1比例尺,直接取作图区的刻度),标记为M1。
3分钟之后再次记录,目标船方位为333,距离本船6.7海里,记为M2。
又3分钟之后,目标船方位335,距离本船6.5海里,记为M3。
④现在可以通过M1,M2,M3,画出目标船M的相对运动线(RML)
⑤确定目标船的相对速度(SRM)。
首先测量已标示出的M1,M2,M3各点之间的距离。本例中取测M1和M2(选取没有特殊要求)之间的距离,测量结果为1000码,即0.5海里
⑥在时间-距离-速度计算尺上表示出时间(3分钟),距离(0.5海里),2点决定一条直线,所以在速度一行的数据即为目标船的相对运动速度(SMR):10节
注意:此时得出的只是目标船M的相对航速,并非真实航速。
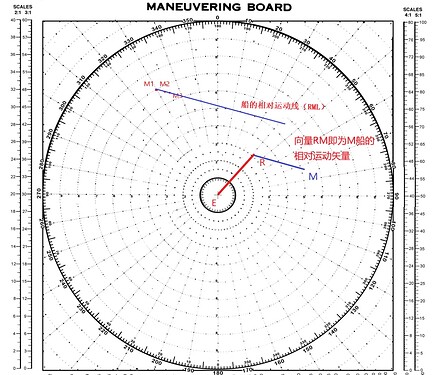
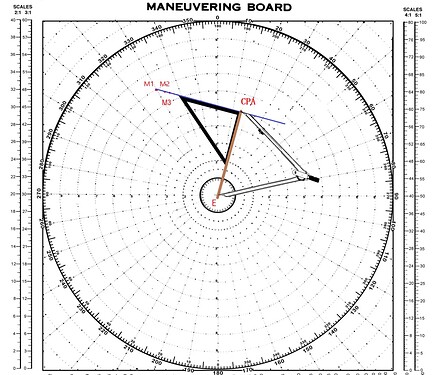
⑦绘制本船与目标船之间的矢量三角,以R为起点做平行于M船的RML的矢量(长度为M船的相对运动速度10,比例尺同样选用5:1),此时的RM即为M船的相对运动矢量
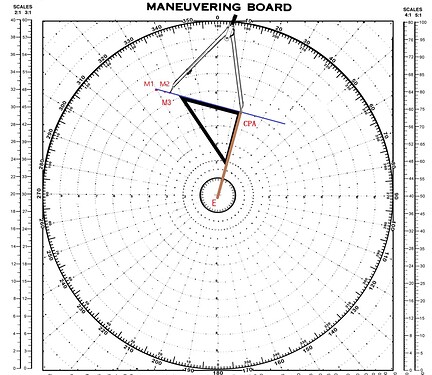
⑧根据矢量三角的运算法则,此时EM即为M船的真运动矢量(真实航向073),测量EM的长度,即为M船的真实航速,本例为23节(依然使用5:1比列尺进行测量)最后,得出M船的真航向为073,真实航速为23节
附加问题,计算E船与M船的CPA,达到CPA的时间
①首先过E点作RML的垂线,与RML的交点即为CPA,测量E点到CPA间的距离为5海里
②测量船M到CPA的距离,即M3与CPA点的距离,结果为3.5海里(注意还是用1:1比例尺)。
③目前已知M到CPA的距离,以及M的相对运动速度(SRM)为10节,在时间-距离-速度计算尺上得出时间15,即为M船在航行15分钟后离本船E距离最近
(四)习题
1.状况
本船E在航向过程中探测到某船M,其时间点与相距本船的距离如下
M1 0908--275˚ ,12000码
M2 0913--270˚,10700码
M3 0916--266˚,10000码
M4 0920--260˚ ,9000码
2.要求:
(1) 绘制出M船的DRM
(2) M船的SRM
(3) CPA
(4) 预测M船到达CPA的时间
3.解答:
(略)
(全篇完)